A Point of Intersection: Geometric and Legal Reasoning

Introduction

Math may evoke strong reactions, specifically geometry. Students have varied responses ranging from feelings of joy to feelings of resentment. Those who love math and geometry may go on to pursue their education in a mathematics based field. Those who despise the subject and cannot fathom having to look at it again may have longed to be rid of the content and enter careers that do not associate with mathematics. Members of the legal profession share a theory that math is not a lawyer’s strength, and that mathematics is not associated with law, according to Maria Termini. However, mathematical reasoning and legal reasoning are closely related, more like siblings, rather than distant cousins, raised by their parents, logic and reasoning. The reasoning attributed to the decisions in the criminal and family law cases, People v. James Robbins (2005) and Smith v. Smith (2009), respectively, can be arranged in familiar mathematical proof styles. Geometric reasoning and legal reasoning share the same reasoning, intentions, and structure.

Similarities

A significant overlap exists between geometric and legal reasoning:

• Identical reasoning
  
  1. Deductive reasoning
  2. Inductive reasoning
  3. Syllogism
• Shared purposes
  
  1. Persuade a majority
  2. Expand and contribute knowledge in the domain
  3. Educate future generations
• Comparable organizational structures
  
  • Geometric
    
    1. Two-column proof
    2. Paragraph Proof
       
       • Direct proof
       • Indirect proof
       • Proof by contradiction
       • Proof by contraposition
       • Proof by cases
  • Legal
    
    1. Issue, Rule, Application, and Conclusion (IRAC)

Case 1: People v. James Robbins (2005)

The New York Court of Appeals held a hearing to determine if Robbins was selling drugs within 1,000 feet of Holy Cross grade school.

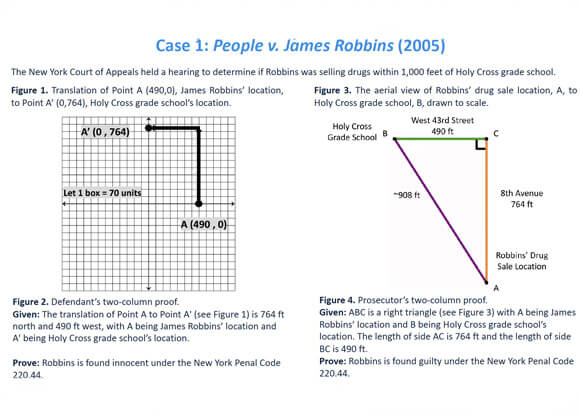
Figure 1. Translation of Point A (490,0), James Robbins’ location, to Point A’ (0,764), Holy Cross grade school’s location.

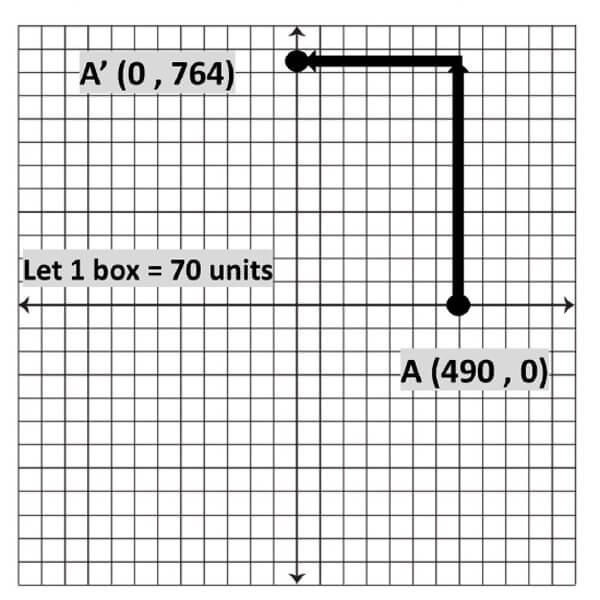
Figure 2. Defendant’s two-column proof.

Given: The translation of Point A to Point A' (see Figure 1) is 764 ft north and 490 ft west, with A being James Robbins’ location and A' being Holy Cross grade school’s location.

Prove: Robbins is found innocent under the New York Penal Code 220.44.

Figure 3. The aerial view of Robbins’ drug sale location, A, to Holy Cross grade school, B, drawn to scale.

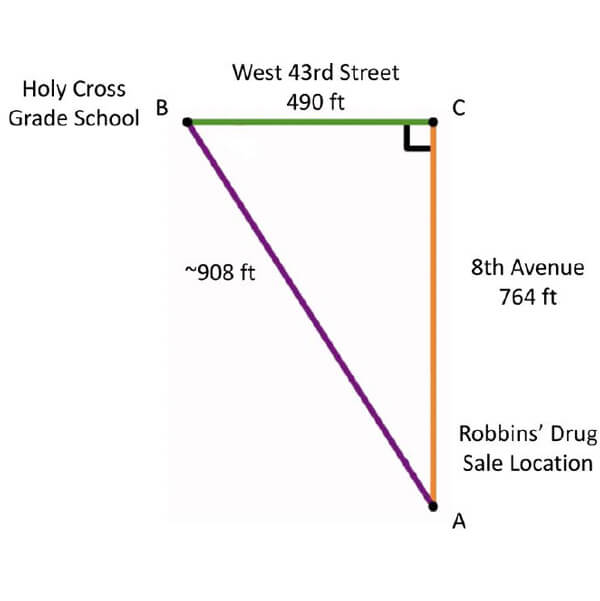
Figure 4. Prosecutor’s two-column proof.

Given: ABC is a right triangle (see Figure 3) with A being James Robbins’ location and B being Holy Cross grade school’s location. The length of side AC is 764 ft and the length of side BC is 490 ft.

Prove: Robbins is found guilty under the New York Penal Code 220.44.

Case 2: Smith v. Smith (2009)

Original Statement: Paulette Andrews Smith and Todd Martin Smith did not establish a common-law marriage.

Proof by Contradiction: Assume Paulette Andrews Smith and Todd Martin Smith established a common law marriage.

Given: The couple began living together in January 1990, after meeting a few months prior in September of 1989, they consensually split household bills evenly, and Todd’s finances were managed by his supposed wife, yet no joint accounts were maintained. Thus, Paulette was responsible for paying Todd’s bills and child support payments from his previous marriage and paid his income tax returns despite them being filed separately. The automobile policy was solely in Todd’s name, but Paulette was a driver on the insurance policy. Paulette completed two loans consigned by Todd in 1998 and 1999, Paulette wrote that she was single on a petition for bankruptcy in 2002, and when Todd applied for a mortgage, Paulette was nowhere written as a co-owner on the real estate deeds.

Then, these facts support “‘evidence that the parties seriously intended to enter into the husband-wife relationship’” which is necessary to hold a true common law marriage as established by Sardonis v. Sardonis (1970).

Secondly, witnesses had opposing opinions. Todd, as well as his ex-wife, sister, and mother, did not view the couple as a married one. Contrarily, Paulette and her daughter and her son’s counselor thought of them as married.

So, this is a contradiction since a valid common-law marriage is having “‘of such a character as to lead to a belief in the community that they were married’” after the decision in Williams v. Herrick (1899). The witnesses who testified had “‘mixed and…different interpretations.” It would have been considered a common-law marriage if everyone agreed that they were married.

Therefore, Paulette and Todd Smith did not have a common-law marriage since there is a contradiction.

Since the assumption is false, the original statement is true: Paulette Andrews Smith and Todd Martin Smith did not establish a common-law marriage.

Future Directions

Common Core revamped math education for students and made the focus “‘about thinking, reasoning, making sense, and communicating.’” Two of the eight math standards support students in their mathematical and legal communication: “(1) constructing viable arguments and critiquing the reasoning of others and (2) attending to precision.” Geometry teaches students to be exact in constructions, transformations, and proofs. Every law student has taken high school geometry, so they have some background in that reasoning which can be transferred to their law courses. College mathematics improves the reasoning process through theorems and their proofs which produce mathematicians. Law students face a parallel to this pedagogical approach in training to think like lawyers with IRAC. Therefore, math and law professors should explore the potentials that lie from fusing their fields.

For Further Discussion

This serves as an overview of the project and does not include the complete work. To further discuss this project, please email Anna Dulberg.

Course Overview

MA 490: Mathematics Senior Seminar is the capstone course for mathematics majors. Students work on a senior-level project, culminating in a written and oral report.

Explore Our Areas of Interest

We've sorted each of our undergraduate, graduate and doctoral programs into unique Areas of Interest. Explore these categories to discover which programs and delivery methods best align with your educational and career goals.

Explore Data and Analytics at Quinnipiac

Explore STEM-Designated Programs at Quinnipiac